RosettaDock

Protein–Protein Docking with Backbone Flexibility

Chu Wang, Philip Bradley and David Baker 2007

Sampling of variable degrees of freedom

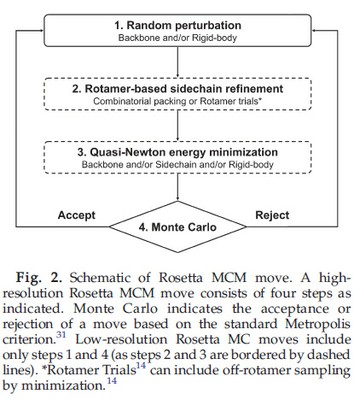
The degrees of freedom allowed to vary in the fold tree can be sampled at several different levels in the Rosetta modeling process (Fig. 2). Conformational sampling in Rosetta is first carried out at a low resolution stage in which fragment insertion and rigid-body Monte Carlo (MC) search are used to rapidly survey the backbone torsional and rigid-body space, respectively, to generate starting points for high-resolution all-atom refinement. This step can be skipped if the backbone conformation and/or rigid-body orientation can be approximately determined based on information from homologous structures or experimental constraints. The high resolution refinement protocol consists of 50–300 Monte Carlo minimization (MCM)30 moves. Each MCM move (Fig. 2) consists of (1) a random perturbation to one or more degrees of freedom; (2) discrete global optimization of the side-chain degrees of freedom using a rotamer representation; (3) quasi-Newton minimization of the energy with respect to a specified subset of degrees of freedom and (4) acceptance or rejection of the composite move according to the standard Metropolis criterion.31 Degrees of freedom in which large sampling ranges are desired are explicitly perturbed in step (1) as well as optimized in step (3), while degrees of freedom in which only small “fine tuning” is desired are kept fixed in step (1) and only allowed to vary in the minimization in step (3), which generally introduces only relatively small changes. Thus, within each of the broad clusters of fold trees included in Fig. 1, there are numerous variations that can be chosen based on the problem at hand (Table 1). For example, in Fig. 1f and Table 1, if relatively large hinge variation is expected, perturbation to the  backbone torsion angles in the hinge region can be included in step (1) in addition to rigid body perturbation; whereas if only small changes in hinge angles are expected, the random MC perturbation can be restricted to the rigid-body degrees of freedom and the hinge degrees of freedom are only allowed to vary in the subsequent minimization step.

ROSETTALIGAND: Protein–Small Molecule Docking with Full Side-Chain Flexibility

Jens Meiler1* and David Baker2* 2006

Docking Monte Carlo Minimization Protocol

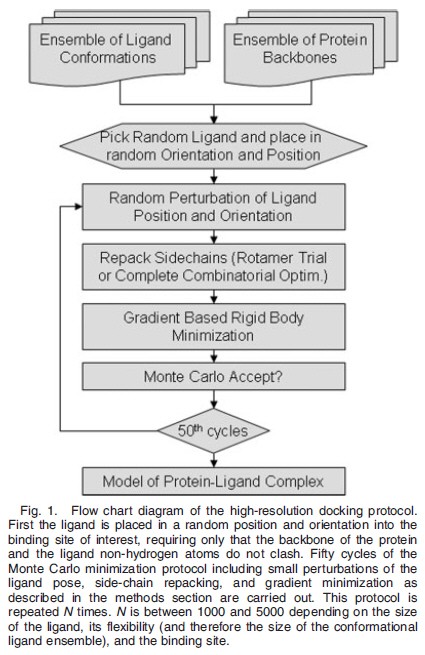
The Monte Carlo minimization protocol (cf. Fig. 1) starts from a random starting position and orientation of the ligand in the binding site of the protein. The ligand center of mass was placed randomly in a cube of (10 A ˚ )3, allowing complete reorientation of the ligand. Each Monte Carlo minimization cycle consists of the following three steps: (1) The position of the ligand is perturbed by random translations of mean 0.1 A ˚ in each direction and by random rotations of mean 0.058 around each axis; (2) side-chain conformations are repacked using either rotamer trials or a full combinatorial search as described below; (3) the rigid body orientation and side-chain v angles of the ligand are optimized using the gradient based Davidson–Fletcher–Powell algorithm. The move (steps 1–3) is accepted based on the difference of staring and final energy according to the standard Metropolis criterion probability P ¼ min{1,exp[(Efinal - Estart/kT]} with kT set to 2 kcal according to the Rosetta energy function. The move is always accepted if the energy decreases, if the energy increases the acceptance probability decreases; because minimization is carried out at each step each move consists of a transition between local minima on the free energy landscape. Each docking trajectory consists of 50 of these Monte Carlo minimization cycles. No simulated annealing was carried out. Between 1000 and 5000 trajectories are computed for each docking experiment.

Ligand Flexibility

An ensemble of ligands was built using the following protocol: (1) a random non-clashing conformation was generated and accepted as first member of the ensemble; (2) 10 new random conformations were generated and their RMSD to all accepted members of the ensemble was evaluated; (3) the conformation with the largest RMSD was added to the accepted set of conformations. Steps (2) and (3) were repeated until 10 conformations were accepted into the ensemble. In step (2) only conformations with a RMSD larger 1 A ˚ to all accepted conformations were considered. If no such conformation could be built, the algorithm was stopped and the conformational ensemble for this particular ligand was left incomplete.